Optimize algebraic systems which describe thermodynamic binding systems

Usage

opti(
  case,
  lowerBounds,
  upperBounds,
  path,
  additionalParameters,
  seed = NULL,
  npop = 40,
  ngen = 200,
  Topology = "random",
  errorThreshold = -Inf,
  add_info = ""
)

Arguments

case: is a character describing which system should be investigated. Either: "dba_host_const", "dba_dye_const", "ida" or "gda".
lowerBounds: is a numeric vector defining the lower boundaries of the parameter. In case of dba_dye_const or *dba_host_const the order of the parameters is: khd, I0, IHD and ID In case of ida and ga the order of the parameters is: kg, I0, IHD and ID.
upperBounds: is a numeric vector defining the upper boundaries of the parameter. The order is the same as for the lower boundaries.
path: is a filepath which contains tabular x-y data. The concentraion of dye or guest respectivly is assumed to be in the first column. Furthermore, should the corresponding signal be stored in the second column. As an alternative an already loaded data.frame can be passed to the function.
additionalParameters: are required parameters which are specific for each case. In case of dba_host_const a numeric vector of length 1 is expected which contains the concentration of the host. In case of dba_dye_const a numeric vector of length 1 is expected which contains the concentration of the dye. In case of ida a numeric vector of length 3 is expected which contains the concentration of the host, dye and the khd parameter. In case of gda a numeric vector of length 3 is expected which contains the concentration of the host, guest and the khd parameter.
seed: is an optional integer argument defining the seed which is set directly for the optimization. In case the argument is not set the current time is used as seed.
npop: is an optional integer argument defining the number of particles during optimization. The default value is set to 40.
ngen: is an optional integer argument defining the number of generations of the particle swarm optimization. The default value is set to 200.
Topology: is an optional character argument defining which topology should be used by the particle swarm algorithm. The options are "star" and "random". The default topology is the "random" topology.
errorThreshold: is an optional numeric argument defining a sufficient small error which acts as a stop signal for the particle swarm algorithm. The default value is set to -Inf.
add_info: is an optional character argument which is printed during optimization

Value

either an instance of ErrorClass if something went wrong. Otherwise the optimized parameter and the insilico signal values are returned.

Examples

path <- paste0(system.file("examples", package = "tsf"), "/IDA.txt")
opti("ida", c(1, 0, 0, 0), c(10^9, 10^6, 10^6, 10^6), path, c(4.3, 6.0, 7079458))
#> Warning: coercing argument of type 'double' to logical
#> Warning: coercing argument of type 'double' to logical
#> [1] ""
#> [1] 2
#> [1] "5.714e+05" "7.649e+01" "1.608e+02" "3.745e-02"
#> [1] "9.680e+00"
#> [1] ""
#> [1] 3
#> [1] "2.129e+08" "5.450e+01" "2.409e+02" "1.018e+02"
#> [1] "9.069e+00"
#> [1] ""
#> [1] 4
#> [1] "7.384e+06" "9.631e-01" "3.978e+02" "1.800e+00"
#> [1] "7.774e+00"
#> [1] ""
#> [1] 5
#> [1] "7.384e+06" "9.631e-01" "3.978e+02" "1.800e+00"
#> [1] "7.774e+00"
#> [1] ""
#> [1] 6
#> [1] "4.430e+07" "2.199e+02" "6.637e+02" "1.000e-15"
#> [1] "5.100e+00"
#> [1] ""
#> [1] 7
#> [1] "4.430e+07" "2.199e+02" "6.637e+02" "1.000e-15"
#> [1] "5.100e+00"
#> [1] ""
#> [1] 8
#> [1] "4.430e+07" "2.199e+02" "6.637e+02" "1.000e-15"
#> [1] "5.100e+00"
#> [1] ""
#> [1] 9
#> [1] "4.430e+07" "2.199e+02" "6.637e+02" "1.000e-15"
#> [1] "5.100e+00"
#> [1] ""
#> [1] 10
#> [1] "4.430e+07" "2.199e+02" "6.637e+02" "1.000e-15"
#> [1] "5.100e+00"
#> [1] ""
#> [1] 11
#> [1] "4.430e+07" "2.199e+02" "6.637e+02" "1.000e-15"
#> [1] "5.100e+00"
#> [1] ""
#> [1] 12
#> [1] "4.430e+07" "2.199e+02" "6.637e+02" "1.000e-15"
#> [1] "5.100e+00"
#> [1] ""
#> [1] 13
#> [1] "3.582e+07" "1.187e+02" "6.825e+02" "1.000e-15"
#> [1] "4.927e+00"
#> [1] ""
#> [1] 14
#> [1] "3.243e+07" "2.487e+01" "6.826e+02" "1.000e-15"
#> [1] "4.661e+00"
#> [1] ""
#> [1] 15
#> [1] "3.243e+07" "2.487e+01" "6.826e+02" "1.000e-15"
#> [1] "4.661e+00"
#> [1] ""
#> [1] 16
#> [1] "3.243e+07" "2.487e+01" "6.826e+02" "1.000e-15"
#> [1] "4.661e+00"
#> [1] ""
#> [1] 17
#> [1] "5.213e+07" "1.321e+01" "1.103e+03" "1.000e-15"
#> [1] "3.295e+00"
#> [1] ""
#> [1] 18
#> [1] "7.596e+07" "1.000e-15" "8.948e+02" "3.482e+01"
#> [1] "3.282e+00"
#> [1] ""
#> [1] 19
#> [1] "7.596e+07" "1.000e-15" "8.948e+02" "3.482e+01"
#> [1] "3.282e+00"
#> [1] ""
#> [1] 20
#> [1] "7.596e+07" "1.000e-15" "8.948e+02" "3.482e+01"
#> [1] "3.282e+00"
#> [1] ""
#> [1] 21
#> [1] "1.370e+08" "1.000e-15" "1.289e+03" "1.319e+01"
#> [1] "2.422e+00"
#> [1] ""
#> [1] 22
#> [1] "1.370e+08" "1.000e-15" "1.289e+03" "1.319e+01"
#> [1] "2.422e+00"
#> [1] ""
#> [1] 23
#> [1] "1.256e+08" "1.000e-15" "1.510e+03" "1.000e-15"
#> [1] "2.212e+00"
#> [1] ""
#> [1] 24
#> [1] "1.256e+08" "1.000e-15" "1.510e+03" "1.000e-15"
#> [1] "2.212e+00"
#> [1] ""
#> [1] 25
#> [1] "1.256e+08" "1.000e-15" "1.510e+03" "1.000e-15"
#> [1] "2.212e+00"
#> [1] ""
#> [1] 26
#> [1] "1.256e+08" "1.000e-15" "1.510e+03" "1.000e-15"
#> [1] "2.212e+00"
#> [1] ""
#> [1] 27
#> [1] "1.256e+08" "1.000e-15" "1.510e+03" "1.000e-15"
#> [1] "2.212e+00"
#> [1] ""
#> [1] 28
#> [1] "1.307e+08" "3.212e+01" "1.537e+03" "1.000e-15"
#> [1] "2.118e+00"
#> [1] ""
#> [1] 29
#> [1] "1.121e+08" "1.269e+02" "1.400e+03" "1.000e-15"
#> [1] "1.780e+00"
#> [1] ""
#> [1] 30
#> [1] "1.121e+08" "1.269e+02" "1.400e+03" "1.000e-15"
#> [1] "1.780e+00"
#> [1] ""
#> [1] 31
#> [1] "1.186e+08" "3.864e+01" "1.363e+03" "1.000e-15"
#> [1] "1.321e+00"
#> [1] ""
#> [1] 32
#> [1] "1.364e+08" "1.000e-15" "1.363e+03" "2.091e+01"
#> [1] "9.583e-01"
#> [1] ""
#> [1] 33
#> [1] "1.364e+08" "1.000e-15" "1.363e+03" "2.091e+01"
#> [1] "9.583e-01"
#> [1] ""
#> [1] 34
#> [1] "1.710e+08" "1.723e+02" "1.366e+03" "1.406e+01"
#> [1] "9.009e-01"
#> [1] ""
#> [1] 35
#> [1] "1.710e+08" "1.723e+02" "1.366e+03" "1.406e+01"
#> [1] "9.009e-01"
#> [1] ""
#> [1] 36
#> [1] "1.416e+08" "2.244e+02" "1.255e+03" "1.000e-15"
#> [1] "5.734e-01"
#> [1] ""
#> [1] 37
#> [1] "1.416e+08" "2.244e+02" "1.255e+03" "1.000e-15"
#> [1] "5.734e-01"
#> [1] ""
#> [1] 38
#> [1] "1.416e+08" "2.244e+02" "1.255e+03" "1.000e-15"
#> [1] "5.734e-01"
#> [1] ""
#> [1] 39
#> [1] "1.347e+08" "1.314e+02" "1.314e+03" "9.966e+00"
#> [1] "4.670e-01"
#> [1] ""
#> [1] 40
#> [1] "1.347e+08" "1.314e+02" "1.314e+03" "9.966e+00"
#> [1] "4.670e-01"
#> [1] ""
#> [1] 41
#> [1] "1.347e+08" "1.314e+02" "1.314e+03" "9.966e+00"
#> [1] "4.670e-01"
#> [1] ""
#> [1] 42
#> [1] "1.347e+08" "1.314e+02" "1.314e+03" "9.966e+00"
#> [1] "4.670e-01"
#> [1] ""
#> [1] 43
#> [1] "1.347e+08" "1.314e+02" "1.314e+03" "9.966e+00"
#> [1] "4.670e-01"
#> [1] ""
#> [1] 44
#> [1] "1.347e+08" "1.314e+02" "1.314e+03" "9.966e+00"
#> [1] "4.670e-01"
#> [1] ""
#> [1] 45
#> [1] "1.347e+08" "1.314e+02" "1.314e+03" "9.966e+00"
#> [1] "4.670e-01"
#> [1] ""
#> [1] 46
#> [1] "1.347e+08" "1.314e+02" "1.314e+03" "9.966e+00"
#> [1] "4.670e-01"
#> [1] ""
#> [1] 47
#> [1] "1.347e+08" "1.314e+02" "1.314e+03" "9.966e+00"
#> [1] "4.670e-01"
#> [1] ""
#> [1] 48
#> [1] "1.347e+08" "1.314e+02" "1.314e+03" "9.966e+00"
#> [1] "4.670e-01"
#> [1] ""
#> [1] 49
#> [1] "1.347e+08" "1.314e+02" "1.314e+03" "9.966e+00"
#> [1] "4.670e-01"
#> [1] ""
#> [1] 50
#> [1] "1.347e+08" "1.314e+02" "1.314e+03" "9.966e+00"
#> [1] "4.670e-01"
#> [1] ""
#> [1] 51
#> [1] "1.347e+08" "1.314e+02" "1.314e+03" "9.966e+00"
#> [1] "4.670e-01"
#> [1] ""
#> [1] 52
#> [1] "1.084e+08" "2.243e+01" "1.298e+03" "1.613e+01"
#> [1] "4.488e-01"
#> [1] ""
#> [1] 53
#> [1] "1.084e+08" "2.243e+01" "1.298e+03" "1.613e+01"
#> [1] "4.488e-01"
#> [1] ""
#> [1] 54
#> [1] "1.084e+08" "2.243e+01" "1.298e+03" "1.613e+01"
#> [1] "4.488e-01"
#> [1] ""
#> [1] 55
#> [1] "1.084e+08" "2.243e+01" "1.298e+03" "1.613e+01"
#> [1] "4.488e-01"
#> [1] ""
#> [1] 56
#> [1] "1.084e+08" "2.243e+01" "1.298e+03" "1.613e+01"
#> [1] "4.488e-01"
#> [1] ""
#> [1] 57
#> [1] "1.084e+08" "2.243e+01" "1.298e+03" "1.613e+01"
#> [1] "4.488e-01"
#> [1] ""
#> [1] 58
#> [1] "1.084e+08" "2.243e+01" "1.298e+03" "1.613e+01"
#> [1] "4.488e-01"
#> [1] ""
#> [1] 59
#> [1] "1.084e+08" "2.243e+01" "1.298e+03" "1.613e+01"
#> [1] "4.488e-01"
#> [1] ""
#> [1] 60
#> [1] "1.084e+08" "2.243e+01" "1.298e+03" "1.613e+01"
#> [1] "4.488e-01"
#> [1] ""
#> [1] 61
#> [1] "1.084e+08" "2.243e+01" "1.298e+03" "1.613e+01"
#> [1] "4.488e-01"
#> [1] ""
#> [1] 62
#> [1] "1.084e+08" "2.243e+01" "1.298e+03" "1.613e+01"
#> [1] "4.488e-01"
#> [1] ""
#> [1] 63
#> [1] "1.084e+08" "2.243e+01" "1.298e+03" "1.613e+01"
#> [1] "4.488e-01"
#> [1] ""
#> [1] 64
#> [1] "1.084e+08" "2.243e+01" "1.298e+03" "1.613e+01"
#> [1] "4.488e-01"
#> [1] ""
#> [1] 65
#> [1] "1.084e+08" "2.243e+01" "1.298e+03" "1.613e+01"
#> [1] "4.488e-01"
#> [1] ""
#> [1] 66
#> [1] "1.084e+08" "2.243e+01" "1.298e+03" "1.613e+01"
#> [1] "4.488e-01"
#> [1] ""
#> [1] 67
#> [1] "1.084e+08" "2.243e+01" "1.298e+03" "1.613e+01"
#> [1] "4.488e-01"
#> [1] ""
#> [1] 68
#> [1] "1.084e+08" "2.243e+01" "1.298e+03" "1.613e+01"
#> [1] "4.488e-01"
#> [1] ""
#> [1] 69
#> [1] "1.084e+08" "2.243e+01" "1.298e+03" "1.613e+01"
#> [1] "4.488e-01"
#> [1] ""
#> [1] 70
#> [1] "1.084e+08" "2.243e+01" "1.298e+03" "1.613e+01"
#> [1] "4.488e-01"
#> [1] ""
#> [1] 71
#> [1] "1.084e+08" "2.243e+01" "1.298e+03" "1.613e+01"
#> [1] "4.488e-01"
#> [1] ""
#> [1] 72
#> [1] "1.084e+08" "2.243e+01" "1.298e+03" "1.613e+01"
#> [1] "4.488e-01"
#> [1] ""
#> [1] 73
#> [1] "1.084e+08" "2.243e+01" "1.298e+03" "1.613e+01"
#> [1] "4.488e-01"
#> [1] ""
#> [1] 74
#> [1] "1.084e+08" "2.243e+01" "1.298e+03" "1.613e+01"
#> [1] "4.488e-01"
#> [1] ""
#> [1] 75
#> [1] "1.084e+08" "2.243e+01" "1.298e+03" "1.613e+01"
#> [1] "4.488e-01"
#> [1] ""
#> [1] 76
#> [1] "1.084e+08" "2.243e+01" "1.298e+03" "1.613e+01"
#> [1] "4.488e-01"
#> [1] ""
#> [1] 77
#> [1] "1.084e+08" "2.243e+01" "1.298e+03" "1.613e+01"
#> [1] "4.488e-01"
#> [1] ""
#> [1] 78
#> [1] "1.084e+08" "2.243e+01" "1.298e+03" "1.613e+01"
#> [1] "4.488e-01"
#> [1] ""
#> [1] 79
#> [1] "1.084e+08" "2.243e+01" "1.298e+03" "1.613e+01"
#> [1] "4.488e-01"
#> [1] ""
#> [1] 80
#> [1] "1.084e+08" "2.243e+01" "1.298e+03" "1.613e+01"
#> [1] "4.488e-01"
#> [1] ""
#> [1] 81
#> [1] "1.084e+08" "2.243e+01" "1.298e+03" "1.613e+01"
#> [1] "4.488e-01"
#> [1] ""
#> [1] 82
#> [1] "1.084e+08" "2.243e+01" "1.298e+03" "1.613e+01"
#> [1] "4.488e-01"
#> [1] ""
#> [1] 83
#> [1] "1.084e+08" "2.243e+01" "1.298e+03" "1.613e+01"
#> [1] "4.488e-01"
#> [1] ""
#> [1] 84
#> [1] "1.084e+08" "2.243e+01" "1.298e+03" "1.613e+01"
#> [1] "4.488e-01"
#> [1] ""
#> [1] 85
#> [1] "1.084e+08" "2.243e+01" "1.298e+03" "1.613e+01"
#> [1] "4.488e-01"
#> [1] ""
#> [1] 86
#> [1] "1.084e+08" "2.243e+01" "1.298e+03" "1.613e+01"
#> [1] "4.488e-01"
#> [1] ""
#> [1] 87
#> [1] "1.084e+08" "2.243e+01" "1.298e+03" "1.613e+01"
#> [1] "4.488e-01"
#> [1] ""
#> [1] 88
#> [1] "1.084e+08" "2.243e+01" "1.298e+03" "1.613e+01"
#> [1] "4.488e-01"
#> [1] ""
#> [1] 89
#> [1] "1.084e+08" "2.243e+01" "1.298e+03" "1.613e+01"
#> [1] "4.488e-01"
#> [1] ""
#> [1] 90
#> [1] "1.084e+08" "2.243e+01" "1.298e+03" "1.613e+01"
#> [1] "4.488e-01"
#> [1] ""
#> [1] 91
#> [1] "1.084e+08" "2.243e+01" "1.298e+03" "1.613e+01"
#> [1] "4.488e-01"
#> [1] ""
#> [1] 92
#> [1] "1.084e+08" "2.243e+01" "1.298e+03" "1.613e+01"
#> [1] "4.488e-01"
#> [1] ""
#> [1] 93
#> [1] "1.084e+08" "2.243e+01" "1.298e+03" "1.613e+01"
#> [1] "4.488e-01"
#> [1] ""
#> [1] 94
#> [1] "1.084e+08" "2.243e+01" "1.298e+03" "1.613e+01"
#> [1] "4.488e-01"
#> [1] ""
#> [1] 95
#> [1] "1.084e+08" "2.243e+01" "1.298e+03" "1.613e+01"
#> [1] "4.488e-01"
#> [1] ""
#> [1] 96
#> [1] "1.084e+08" "2.243e+01" "1.298e+03" "1.613e+01"
#> [1] "4.488e-01"
#> [1] ""
#> [1] 97
#> [1] "1.084e+08" "2.243e+01" "1.298e+03" "1.613e+01"
#> [1] "4.488e-01"
#> [1] ""
#> [1] 98
#> [1] "1.084e+08" "2.243e+01" "1.298e+03" "1.613e+01"
#> [1] "4.488e-01"
#> [1] ""
#> [1] 99
#> [1] "1.084e+08" "2.243e+01" "1.298e+03" "1.613e+01"
#> [1] "4.488e-01"
#> [1] ""
#> [1] 100
#> [1] "1.084e+08" "2.243e+01" "1.298e+03" "1.613e+01"
#> [1] "4.488e-01"
#> [1] ""
#> [1] 101
#> [1] "1.084e+08" "2.243e+01" "1.298e+03" "1.613e+01"
#> [1] "4.488e-01"
#> [1] ""
#> [1] 102
#> [1] "1.084e+08" "2.243e+01" "1.298e+03" "1.613e+01"
#> [1] "4.488e-01"
#> [1] ""
#> [1] 103
#> [1] "1.084e+08" "2.243e+01" "1.298e+03" "1.613e+01"
#> [1] "4.488e-01"
#> [1] ""
#> [1] 104
#> [1] "1.084e+08" "2.243e+01" "1.298e+03" "1.613e+01"
#> [1] "4.488e-01"
#> [1] ""
#> [1] 105
#> [1] "1.084e+08" "2.243e+01" "1.298e+03" "1.613e+01"
#> [1] "4.488e-01"
#> [1] ""
#> [1] 106
#> [1] "1.084e+08" "2.243e+01" "1.298e+03" "1.613e+01"
#> [1] "4.488e-01"
#> [1] ""
#> [1] 107
#> [1] "1.084e+08" "2.243e+01" "1.298e+03" "1.613e+01"
#> [1] "4.488e-01"
#> [1] ""
#> [1] 108
#> [1] "1.084e+08" "2.243e+01" "1.298e+03" "1.613e+01"
#> [1] "4.488e-01"
#> [1] ""
#> [1] 109
#> [1] "1.084e+08" "2.243e+01" "1.298e+03" "1.613e+01"
#> [1] "4.488e-01"
#> [1] ""
#> [1] 110
#> [1] "1.084e+08" "2.243e+01" "1.298e+03" "1.613e+01"
#> [1] "4.488e-01"
#> [1] ""
#> [1] 111
#> [1] "1.084e+08" "2.243e+01" "1.298e+03" "1.613e+01"
#> [1] "4.488e-01"
#> [1] ""
#> [1] 112
#> [1] "1.084e+08" "2.243e+01" "1.298e+03" "1.613e+01"
#> [1] "4.488e-01"
#> [1] ""
#> [1] 113
#> [1] "1.084e+08" "2.243e+01" "1.298e+03" "1.613e+01"
#> [1] "4.488e-01"
#> [1] ""
#> [1] 114
#> [1] "1.084e+08" "2.243e+01" "1.298e+03" "1.613e+01"
#> [1] "4.488e-01"
#> [1] ""
#> [1] 115
#> [1] "1.084e+08" "2.243e+01" "1.298e+03" "1.613e+01"
#> [1] "4.488e-01"
#> [1] ""
#> [1] 116
#> [1] "1.084e+08" "2.243e+01" "1.298e+03" "1.613e+01"
#> [1] "4.488e-01"
#> [1] ""
#> [1] 117
#> [1] "1.084e+08" "2.243e+01" "1.298e+03" "1.613e+01"
#> [1] "4.488e-01"
#> [1] ""
#> [1] 118
#> [1] "1.084e+08" "2.243e+01" "1.298e+03" "1.613e+01"
#> [1] "4.488e-01"
#> [1] ""
#> [1] 119
#> [1] "1.084e+08" "2.243e+01" "1.298e+03" "1.613e+01"
#> [1] "4.488e-01"
#> [1] ""
#> [1] 120
#> [1] "1.084e+08" "2.243e+01" "1.298e+03" "1.613e+01"
#> [1] "4.488e-01"
#> [1] ""
#> [1] 121
#> [1] "1.084e+08" "2.243e+01" "1.298e+03" "1.613e+01"
#> [1] "4.488e-01"
#> [1] ""
#> [1] 122
#> [1] "1.084e+08" "2.243e+01" "1.298e+03" "1.613e+01"
#> [1] "4.488e-01"
#> [1] ""
#> [1] 123
#> [1] "1.084e+08" "2.243e+01" "1.298e+03" "1.613e+01"
#> [1] "4.488e-01"
#> [1] ""
#> [1] 124
#> [1] "1.084e+08" "2.243e+01" "1.298e+03" "1.613e+01"
#> [1] "4.488e-01"
#> [1] ""
#> [1] 125
#> [1] "1.084e+08" "2.243e+01" "1.298e+03" "1.613e+01"
#> [1] "4.488e-01"
#> [1] ""
#> [1] 126
#> [1] "1.084e+08" "2.243e+01" "1.298e+03" "1.613e+01"
#> [1] "4.488e-01"
#> [1] ""
#> [1] 127
#> [1] "1.084e+08" "2.243e+01" "1.298e+03" "1.613e+01"
#> [1] "4.488e-01"
#> [1] ""
#> [1] 128
#> [1] "1.084e+08" "2.243e+01" "1.298e+03" "1.613e+01"
#> [1] "4.488e-01"
#> [1] ""
#> [1] 129
#> [1] "1.084e+08" "2.243e+01" "1.298e+03" "1.613e+01"
#> [1] "4.488e-01"
#> [1] ""
#> [1] 130
#> [1] "1.084e+08" "2.243e+01" "1.298e+03" "1.613e+01"
#> [1] "4.488e-01"
#> [1] ""
#> [1] 131
#> [1] "1.168e+08" "1.281e+02" "1.278e+03" "1.000e-15"
#> [1] "3.918e-01"
#> [1] ""
#> [1] 132
#> [1] "1.168e+08" "1.281e+02" "1.278e+03" "1.000e-15"
#> [1] "3.918e-01"
#> [1] ""
#> [1] 133
#> [1] "1.168e+08" "1.281e+02" "1.278e+03" "1.000e-15"
#> [1] "3.918e-01"
#> [1] ""
#> [1] 134
#> [1] "1.168e+08" "1.281e+02" "1.278e+03" "1.000e-15"
#> [1] "3.918e-01"
#> [1] ""
#> [1] 135
#> [1] "1.168e+08" "1.281e+02" "1.278e+03" "1.000e-15"
#> [1] "3.918e-01"
#> [1] ""
#> [1] 136
#> [1] "1.168e+08" "1.281e+02" "1.278e+03" "1.000e-15"
#> [1] "3.918e-01"
#> [1] ""
#> [1] 137
#> [1] "1.168e+08" "1.281e+02" "1.278e+03" "1.000e-15"
#> [1] "3.918e-01"
#> [1] ""
#> [1] 138
#> [1] "1.168e+08" "1.281e+02" "1.278e+03" "1.000e-15"
#> [1] "3.918e-01"
#> [1] ""
#> [1] 139
#> [1] "1.168e+08" "1.281e+02" "1.278e+03" "1.000e-15"
#> [1] "3.918e-01"
#> [1] ""
#> [1] 140
#> [1] "1.168e+08" "1.281e+02" "1.278e+03" "1.000e-15"
#> [1] "3.918e-01"
#> [1] ""
#> [1] 141
#> [1] "1.168e+08" "1.281e+02" "1.278e+03" "1.000e-15"
#> [1] "3.918e-01"
#> [1] ""
#> [1] 142
#> [1] "1.168e+08" "1.281e+02" "1.278e+03" "1.000e-15"
#> [1] "3.918e-01"
#> [1] ""
#> [1] 143
#> [1] "1.168e+08" "1.281e+02" "1.278e+03" "1.000e-15"
#> [1] "3.918e-01"
#> [1] ""
#> [1] 144
#> [1] "1.168e+08" "1.281e+02" "1.278e+03" "1.000e-15"
#> [1] "3.918e-01"
#> [1] ""
#> [1] 145
#> [1] "1.168e+08" "1.281e+02" "1.278e+03" "1.000e-15"
#> [1] "3.918e-01"
#> [1] ""
#> [1] 146
#> [1] "1.168e+08" "1.281e+02" "1.278e+03" "1.000e-15"
#> [1] "3.918e-01"
#> [1] ""
#> [1] 147
#> [1] "1.168e+08" "1.281e+02" "1.278e+03" "1.000e-15"
#> [1] "3.918e-01"
#> [1] ""
#> [1] 148
#> [1] "1.168e+08" "1.281e+02" "1.278e+03" "1.000e-15"
#> [1] "3.918e-01"
#> [1] ""
#> [1] 149
#> [1] "1.168e+08" "1.281e+02" "1.278e+03" "1.000e-15"
#> [1] "3.918e-01"
#> [1] ""
#> [1] 150
#> [1] "1.168e+08" "1.281e+02" "1.278e+03" "1.000e-15"
#> [1] "3.918e-01"
#> [1] ""
#> [1] 151
#> [1] "1.168e+08" "1.281e+02" "1.278e+03" "1.000e-15"
#> [1] "3.918e-01"
#> [1] ""
#> [1] 152
#> [1] "1.168e+08" "1.281e+02" "1.278e+03" "1.000e-15"
#> [1] "3.918e-01"
#> [1] ""
#> [1] 153
#> [1] "1.168e+08" "1.281e+02" "1.278e+03" "1.000e-15"
#> [1] "3.918e-01"
#> [1] ""
#> [1] 154
#> [1] "1.168e+08" "1.281e+02" "1.278e+03" "1.000e-15"
#> [1] "3.918e-01"
#> [1] ""
#> [1] 155
#> [1] "1.168e+08" "1.281e+02" "1.278e+03" "1.000e-15"
#> [1] "3.918e-01"
#> [1] ""
#> [1] 156
#> [1] "1.168e+08" "1.281e+02" "1.278e+03" "1.000e-15"
#> [1] "3.918e-01"
#> [1] ""
#> [1] 157
#> [1] "1.168e+08" "1.281e+02" "1.278e+03" "1.000e-15"
#> [1] "3.918e-01"
#> [1] ""
#> [1] 158
#> [1] "1.168e+08" "1.281e+02" "1.278e+03" "1.000e-15"
#> [1] "3.918e-01"
#> [1] ""
#> [1] 159
#> [1] "1.168e+08" "1.281e+02" "1.278e+03" "1.000e-15"
#> [1] "3.918e-01"
#> [1] ""
#> [1] 160
#> [1] "1.168e+08" "1.281e+02" "1.278e+03" "1.000e-15"
#> [1] "3.918e-01"
#> [1] ""
#> [1] 161
#> [1] "1.168e+08" "1.281e+02" "1.278e+03" "1.000e-15"
#> [1] "3.918e-01"
#> [1] ""
#> [1] 162
#> [1] "1.168e+08" "1.281e+02" "1.278e+03" "1.000e-15"
#> [1] "3.918e-01"
#> [1] ""
#> [1] 163
#> [1] "1.168e+08" "1.281e+02" "1.278e+03" "1.000e-15"
#> [1] "3.918e-01"
#> [1] ""
#> [1] 164
#> [1] "1.168e+08" "1.281e+02" "1.278e+03" "1.000e-15"
#> [1] "3.918e-01"
#> [1] ""
#> [1] 165
#> [1] "1.168e+08" "1.281e+02" "1.278e+03" "1.000e-15"
#> [1] "3.918e-01"
#> [1] ""
#> [1] 166
#> [1] "1.168e+08" "1.281e+02" "1.278e+03" "1.000e-15"
#> [1] "3.918e-01"
#> [1] ""
#> [1] 167
#> [1] "1.168e+08" "1.281e+02" "1.278e+03" "1.000e-15"
#> [1] "3.918e-01"
#> [1] ""
#> [1] 168
#> [1] "1.168e+08" "1.281e+02" "1.278e+03" "1.000e-15"
#> [1] "3.918e-01"
#> [1] ""
#> [1] 169
#> [1] "1.168e+08" "1.281e+02" "1.278e+03" "1.000e-15"
#> [1] "3.918e-01"
#> [1] ""
#> [1] 170
#> [1] "1.168e+08" "1.281e+02" "1.278e+03" "1.000e-15"
#> [1] "3.918e-01"
#> [1] ""
#> [1] 171
#> [1] "1.168e+08" "1.281e+02" "1.278e+03" "1.000e-15"
#> [1] "3.918e-01"
#> [1] ""
#> [1] 172
#> [1] "1.168e+08" "1.281e+02" "1.278e+03" "1.000e-15"
#> [1] "3.918e-01"
#> [1] ""
#> [1] 173
#> [1] "1.168e+08" "1.281e+02" "1.278e+03" "1.000e-15"
#> [1] "3.918e-01"
#> [1] ""
#> [1] 174
#> [1] "1.168e+08" "1.281e+02" "1.278e+03" "1.000e-15"
#> [1] "3.918e-01"
#> [1] ""
#> [1] 175
#> [1] "1.168e+08" "1.281e+02" "1.278e+03" "1.000e-15"
#> [1] "3.918e-01"
#> [1] ""
#> [1] 176
#> [1] "1.168e+08" "1.281e+02" "1.278e+03" "1.000e-15"
#> [1] "3.918e-01"
#> [1] ""
#> [1] 177
#> [1] "1.168e+08" "1.281e+02" "1.278e+03" "1.000e-15"
#> [1] "3.918e-01"
#> [1] ""
#> [1] 178
#> [1] "1.168e+08" "1.281e+02" "1.278e+03" "1.000e-15"
#> [1] "3.918e-01"
#> [1] ""
#> [1] 179
#> [1] "1.168e+08" "1.281e+02" "1.278e+03" "1.000e-15"
#> [1] "3.918e-01"
#> [1] ""
#> [1] 180
#> [1] "1.168e+08" "1.281e+02" "1.278e+03" "1.000e-15"
#> [1] "3.918e-01"
#> [1] ""
#> [1] 181
#> [1] "1.168e+08" "1.281e+02" "1.278e+03" "1.000e-15"
#> [1] "3.918e-01"
#> [1] ""
#> [1] 182
#> [1] "1.168e+08" "1.281e+02" "1.278e+03" "1.000e-15"
#> [1] "3.918e-01"
#> [1] ""
#> [1] 183
#> [1] "1.168e+08" "1.281e+02" "1.278e+03" "1.000e-15"
#> [1] "3.918e-01"
#> [1] ""
#> [1] 184
#> [1] "1.168e+08" "1.281e+02" "1.278e+03" "1.000e-15"
#> [1] "3.918e-01"
#> [1] ""
#> [1] 185
#> [1] "1.168e+08" "1.281e+02" "1.278e+03" "1.000e-15"
#> [1] "3.918e-01"
#> [1] ""
#> [1] 186
#> [1] "1.168e+08" "1.281e+02" "1.278e+03" "1.000e-15"
#> [1] "3.918e-01"
#> [1] ""
#> [1] 187
#> [1] "1.168e+08" "1.281e+02" "1.278e+03" "1.000e-15"
#> [1] "3.918e-01"
#> [1] ""
#> [1] 188
#> [1] "1.168e+08" "1.281e+02" "1.278e+03" "1.000e-15"
#> [1] "3.918e-01"
#> [1] ""
#> [1] 189
#> [1] "1.168e+08" "1.281e+02" "1.278e+03" "1.000e-15"
#> [1] "3.918e-01"
#> [1] ""
#> [1] 190
#> [1] "1.168e+08" "1.281e+02" "1.278e+03" "1.000e-15"
#> [1] "3.918e-01"
#> [1] ""
#> [1] 191
#> [1] "1.168e+08" "1.281e+02" "1.278e+03" "1.000e-15"
#> [1] "3.918e-01"
#> [1] ""
#> [1] 192
#> [1] "1.168e+08" "1.281e+02" "1.278e+03" "1.000e-15"
#> [1] "3.918e-01"
#> [1] ""
#> [1] 193
#> [1] "1.168e+08" "1.281e+02" "1.278e+03" "1.000e-15"
#> [1] "3.918e-01"
#> [1] ""
#> [1] 194
#> [1] "1.168e+08" "1.281e+02" "1.278e+03" "1.000e-15"
#> [1] "3.918e-01"
#> [1] ""
#> [1] 195
#> [1] "1.168e+08" "1.281e+02" "1.278e+03" "1.000e-15"
#> [1] "3.918e-01"
#> [1] ""
#> [1] 196
#> [1] "1.168e+08" "1.281e+02" "1.278e+03" "1.000e-15"
#> [1] "3.918e-01"
#> [1] ""
#> [1] 197
#> [1] "1.168e+08" "1.281e+02" "1.278e+03" "1.000e-15"
#> [1] "3.918e-01"
#> [1] ""
#> [1] 198
#> [1] "1.168e+08" "1.281e+02" "1.278e+03" "1.000e-15"
#> [1] "3.918e-01"
#> [1] ""
#> [1] 199
#> [1] "1.168e+08" "1.281e+02" "1.278e+03" "1.000e-15"
#> [1] "3.918e-01"
#> [1] ""
#> [1] 200
#> [1] "1.168e+08" "1.281e+02" "1.278e+03" "1.000e-15"
#> [1] "3.918e-01"
#> $data
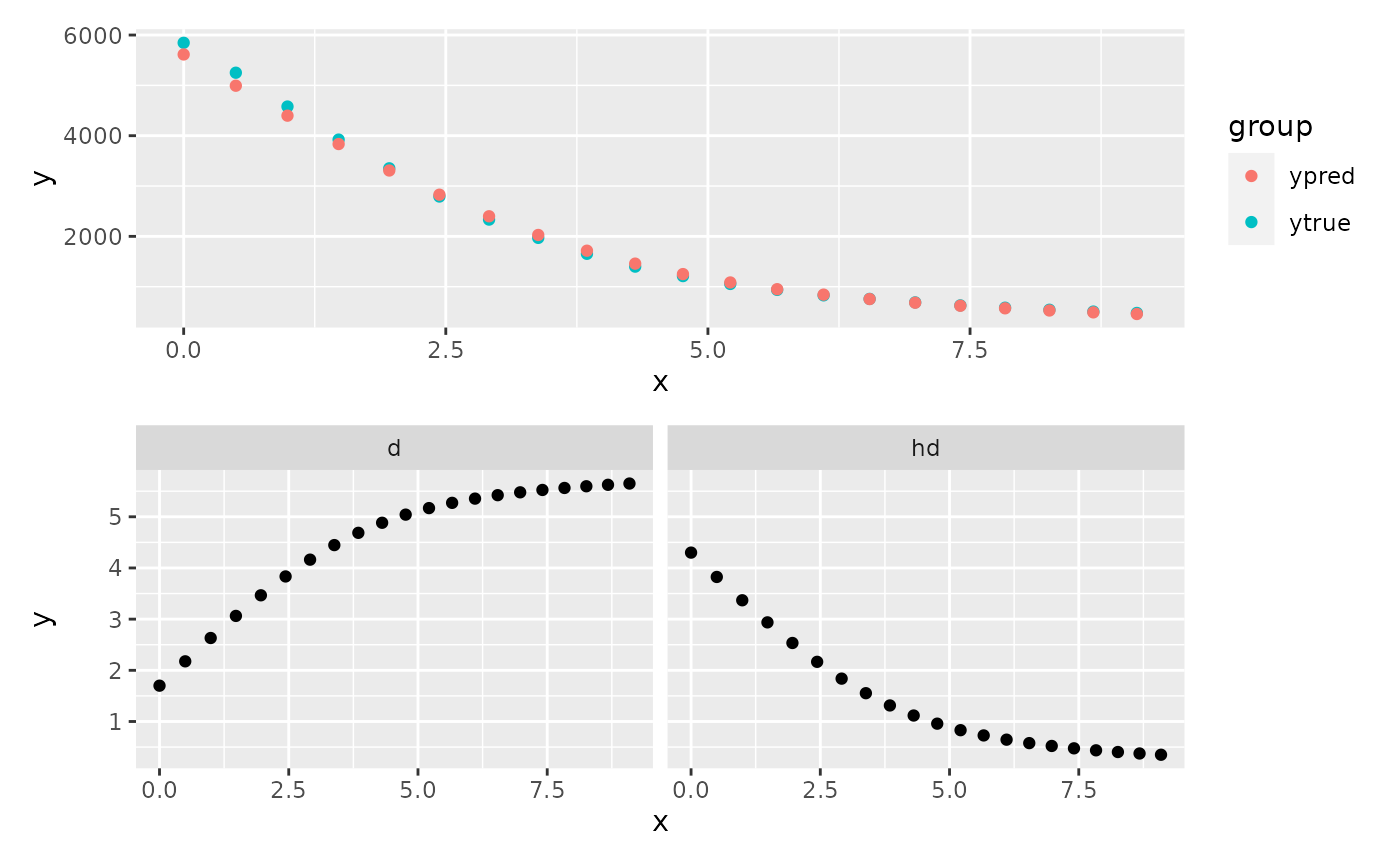
#>    total Guest measured [M] Signal measured Signal simulated
#> 1                    0.0000        5846.100        5622.0429
#> 2                    0.4975        5251.420        5007.6758
#> 3                    0.9901        4579.220        4414.7313
#> 4                    1.4778        3922.710        3848.0011
#> 5                    1.9608        3351.840        3313.6293
#> 6                    2.4390        2791.560        2819.7648
#> 7                    2.9126        2333.070        2375.3154
#> 8                    3.3816        1969.980        1988.7158
#> 9                    3.8462        1653.070        1664.7563
#> 10                   4.3062        1398.690        1402.7152
#> 11                   4.7619        1210.670        1195.9004
#> 12                   5.2133        1054.340        1034.6581
#> 13                   5.6604         936.536         908.9962
#> 14                   6.1033         827.836         810.2767
#> 15                   6.5421         757.271         731.7506
#> 16                   6.9767         687.888         668.4170
#> 17                   7.4074         628.260         616.5686
#> 18                   7.8341         582.921         573.5521
#> 19                   8.2569         541.771         537.4030
#> 20                   8.6758         505.525         506.6748
#> 21                   9.0909         478.098         480.2767
#>    free Dye simulated [M] Host-Dye simulated [M]
#> 1                1.700000              4.2999996
#> 2                2.180856              3.8191442
#> 3                2.644944              3.3550559
#> 4                3.088515              2.9114851
#> 5                3.506759              2.4932408
#> 6                3.893299              2.1067008
#> 7                4.241163              1.7588373
#> 8                4.543748              1.4562519
#> 9                4.797306              1.2026940
#> 10               5.002401              0.9975985
#> 11               5.164272              0.8357279
#> 12               5.290474              0.7095260
#> 13               5.388827              0.6111725
#> 14               5.466094              0.5339063
#> 15               5.527555              0.4724451
#> 16               5.577125              0.4228750
#> 17               5.617706              0.3822940
#> 18               5.651374              0.3486257
#> 19               5.679668              0.3203324
#> 20               5.703718              0.2962819
#> 21               5.724380              0.2756205
#> 
#> $parameter
#>   Ka(HG) [1/M]     I(0) I(HD) [1/M] I(D) [1/M]
#> 1    116790111 128.1289    1277.655      1e-15
#> 
#> $plot

#> 
#> $metrices
#>   MeanSquareError RootMeanSquareError MeanAbsoluteError        R2 R2 adjusted
#> 1        7130.814            84.44415          47.78123 0.9991971   0.9991548
#> 
#> $seed
#> [1] 1732615580
#> 
#> $additionalParameters
#>     Host [M]      Dye [M] Ka(HD) [1/M] 
#>          4.3          6.0    7079458.0 
#> 
#> $lowerBounds
#> Ka(HG) [1/M]         I(0)  I(HD) [1/M]   I(D) [1/M] 
#>            1            0            0            0 
#> 
#> $upperBounds
#> Ka(HG) [1/M]         I(0)  I(HD) [1/M]   I(D) [1/M] 
#>        1e+09        1e+06        1e+06        1e+06 
#> 
#> $npop
#> [1] 40
#> 
#> $ngen
#> [1] 200
#> 
#> $Topology
#> [1] "random"
#>